Dangerously irrelevant operator
In statistical mechanics and quantum field theory, a dangerously irrelevant operator (or dangerous irrelevant operator) is an operator which is irrelevant, yet affects the infrared physics significantly because the vacuum expectation value of some field depends sensitively upon the dangerously irrelevant operator.
Example
Let us suppose there is a field  with a potential depending upon two parameters, a and b.
with a potential depending upon two parameters, a and b.
Let us also suppose that a is positive and nonzero and  >
>  . If b is zero, there is no stable equilibrium. If the scaling dimension of
. If b is zero, there is no stable equilibrium. If the scaling dimension of  is c, then the scaling dimension of b is
is c, then the scaling dimension of b is  where d is the number of dimensions. It is clear that if the scaling dimension of b is negative, b is an irrelevant parameter. However, the crucial point is, that the
where d is the number of dimensions. It is clear that if the scaling dimension of b is negative, b is an irrelevant parameter. However, the crucial point is, that the 
 .
.
depends very sensitively upon b, at least for small values of b. Because the nature of the IR physics also depends upon the  , the IR physics looks very different even for a tiny change in b not because the physics in the vicinity of
, the IR physics looks very different even for a tiny change in b not because the physics in the vicinity of 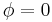 changes much — it hardly changes at all — but because the
changes much — it hardly changes at all — but because the  we are expanding about has changed enormously.
we are expanding about has changed enormously.
In supersymmetric models with a modulus, we can often have dangerously irrelevant parameters.
References
Amit, D.; Peliti, L. (1982). "On dangerous irrelevant operators". Annals of Physics 140: 207−231. Bibcode 1982AnPhy.140..207A. doi:10.1016/0003-4916(82)90159-2.
